|
"The majority of players are looking for reasons to fold. I am looking for reasons to play." ~ Daniel Negreanu The Rule of 2 and 4 are quick shortcuts to help us work out the percentage needed to get a draw in Texas No-Limit Hold'em. These shortcuts aren’t exact. However, they are good enough for doing quick probabilities in our head at the tables.
The Rule of 2 The Rule of 2 states: Multiply your number of outs by 2 to get the approximate percentage of a draw you have on the turn or the river. For example, let's say you have a flush draw after the flop.
The Rule of 2 works because there are 52 cards in the deck and 52 goes into one hundred approximately twice. The Rule of 4 The Rule of 4 is used when you are considering an all-in move after the flop and will see both the turn and river cards. Multiply your number of outs by 4 to get the approximate percentage of a draw. Like the Rule of 2 example, you have a flush draw after the flop.
Once again, that’s close and useful for quick estimate at the tables. Note: The Core Math Chapter of Mastering Poker Math provides more detail on how this equation is derived.
0 Comments
Pot odds and implied odds are major concepts in the math of poker. It is crucial to know when the odds are in your favor, and when they are against you. Then, you can make informed decisions on when to call, bet, fold, raise, re-raise or go all-in. Note: For the examples in this section, round numbers will used (whenever possible). It is easier to learn a concept in black and white. The real world runs in shades of gray. Consequently, at the poker tables you will need to approximate. Pot Odds Pot odds are the ratio of the current size of the pot to the cost of a contemplated call. For example, if there is $7,500 in a pot and villain (an opponent) bets $2,500. There is now $10,000 in the pot. It will cost you $2,500 to win a potential $10,000. If you bet there will be $12,500 in the pot. Your pot odds are 20% ($2,500/$12,500). You must win 1 out of 5 pots to break even. This can be expressed as 1:4. That is to say, you must win one pot and can lose four pots to break even. If you win more than that, you will make money. When the odds of drawing a card that wins the pot are higher than the pot odds, the call has a positive expectation. In other words, on average, you will win more money than the cost of the bet. Conversely, if the odds of drawing a winning card are numerically lower than the pot odds, the call has a negative expectation. On average, you will win less money than the cost of the bet. To explain this concept further let’s review a flush draw. Sometimes this is called chasing a flush. Example #1: Getting Pot Odds on a Flush Draw
Implied Odds Implied odds are your potential winnings by the end of the hand compared with the amount of money required to make a call. They are different than pot odds because they account for possible future betting. Implied odds are calculated in situations where you have a draw. You expect to make money on additional bets if your draw is made. And, you can fold to a bet on the next card if the pot and implied odds are unfavorable. Since you expect to gain additional money in a later round, or rounds (if your draw is made, and not be committed to lose additional bets when your draw is missed), the extra money you expect to gain is added to the current pot size. What you may gain is only an estimate depending on your read of the other player. It isn’t an exact science. Example #2: Getting Implied Odds on a Flush Draw
To learn more please go to the: Mastering Poker Math Book Copyright 2021
Charles W. Clayton All Rights Reserved "Poker is a skill game pretending to be a chance game.” ~ James Altucher The variability in poker is huge. This gives rise to some fascinating characteristics of the game. First, the high variance of the game provides excitement that has some addictive qualities. Second, a high percentage of players think they are better than they are because they can play with excellent players and do okay at times. They play by their gut and rarely (if ever) use the math. The high variability allows them this luxury. And third, there are few (possibly no other) major sports or games where the variability is as high as it is in Texas No-Limit Hold’em. Here are a couple of examples.
The point is that in most sports and games, the top players have an overwhelming advantage (because of small variances) over beginners in the long run, and well as in the short-run. This isn’t the case for No-Limit Hold’em in the short-run. Tight Hand Variances The poker hands in Hold’em have relatively tight hand variances. Here are some examples:
Note: The “s” in these examples means suited. The “o” means non-suited. This convention will be used throughout the text for suited and unsuited cards. There are many more examples. The point is, even the worst hands will win a reasonable percentage of the time against the best hands. It is this tight variance in poker hands which allows bad players to get lucky in the short run and beat good players. This is a major reason why vast numbers of people enjoy playing the game. On any given day even some of the worst players have a slight chance to win. But, not in the long run! The best players will consistently win because the game of Texas No-Limit Hold’em is really a skill game, not a luck game. Self-delusion is common in poker because of occasional runs of good cards and good luck. But good cards dry up, and good luck runs out. Bad beats (low probability events) by bad players are common in poker and cause many tilt related rantings, especially from those who don’t understand the math. Yet, it is just the variance which provide these emotional roller-coaster rides all poker players have experienced time and again. Millions of people play the game because of the high variability allowing them to get lucky at times. They supply massive sums of money for the tournaments fueling the poker boom. The silver lining is that the exceptional players do well over the long run. Although you will have plenty of bad beats (everyone does), in the long run if your math and other parts of your game are solid, you will do better than those who depend on luck, instead of skill as a strategy. So, what is luck? Simply put:
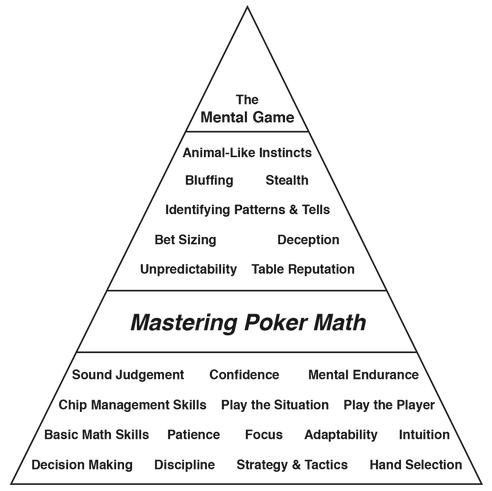
The top players are studious, curious, patient, willing to do the work and always striving to do better. They combine their math skills with their other poker skills and become a feared shark at the poker tables. In our next and final part of the Introduction we will discuss who Mastering Poker Math is for and the overall book layout Make sure you press "Like" if you enjoyed this Blog Post ...and be sure and share it with your friends! In this blog post we will explore the importance of math in poker and why it is worth investing time to become good at it if you are a serious player, or just enjoy knowing a bit more than your friends about the game. Players today are competitive, experienced and better than ever. Gaining a competitive advantage isn’t as easy as it once was, however it is still possible. Knowing the math is a key element. This begs the question: How much of a competitive advantage can math bring you today? I will make an educated guess that poker math is (at least) 40% of the game. It might be more. Someone, or a computer program will probably come out with a better number based on analysis at some point. But for this discussion let’s assume it is 40%. Thus, if the perfect player is 100% Game Theory Optimal (which doesn’t exist, but is fun to think about), and the math is 40% of that, doesn’t it make sense to invest the time to become exceptional at poker math? Especially, when much of the math is straight-forward! If the premise of 40% is correct, then learning 25 - 30% of that math knowledge will give you a significant advantage over others who don’t know or use much math. The reason I say learn 25 - 30% is because there is at least 10 - 15% of the math that is extremely complex. Assuming the average poker player’s math ability is in the 10 - 15% range (the author’s observation), then you will have a significant advantage by knowing 25 - 30% of the math. Many players who consistently make poor Expected Value (EV) plays have inferior math abilities. They don’t size their bets properly by betting too much, or too little. This is done a high percentage of the time. And, they will call over inflated bets when they don’t have enough hand equity to warrant the call. These players can be exploited with excellent math knowledge. To add to this, the variabilities in Texas No-Limit Hold’em are small. In other words, there are thin margins. Consequently: In a game with thin margins and many poor math skilled players, knowing the math provides a significant advantage. Conclusion Texas Hold’em is incredibly popular in the United States and around the world. According to the WPT (World Poker Tour) there are 60 million poker players in the US and 100 million poker players around the world. More people play poker than either golf, tennis or billiards. The Skill Gap in Texas No-Limit Hold’em has dropped dramatically and continues to go down. The competition today is tough. It is very tough! The poker learning curve has been slashed by the amazing number of books, internet, software, videos, blogs, resources and access to live and internet games. Many people invest a lot of their time and money learning and playing the game. However, most still do not know the math at a visceral level. Many players don’t see the value in learning the math. They think it is a game of luck, not skill. Some players detest the math and want to play strictly by their gut. Others are just lazy. Whatever the reason, this opens a huge opportunity door for you. By learning the math at a gut level, you will become part of the New Breed of Poker Player. Math is only one aspect of the game. To become excellent at the game requires many skills. And these skills need to be combined with your math abilities. Shown below is a high-level graphic of some of the key skills to become a feared shark at Texas No-Limit Hold’em. Throughout the book we will discuss how to integrate these skills with the math that is being explained. Skills to Become a Feared Shark at Poker This final blog has completed our series on how to become a New Breed of Poker Player. Stay tuned for more blogs on Mastering Poker Math! Chuck Clayton
Copyright© 2019 All Rights Reserved |
Now available on Amazon.com
"A must read if you’re serious about improving your game."
~ Tom Britton Become a Feared Shark!
This blog has been created to help you gain a competitive edge using poker math and how to integrate it with the rest of your game. Enjoy! ~ Chuck Clayton
Archives
June 2021
Categories
|




 RSS Feed
RSS Feed